Sind Frauen tatsächlich viel risikoaverser als Männer? // #BreakTheBias – auch in der Forschung

Lesezeit: 7 Minuten

Der diesjährige Weltfrauentag am 8. März steht unter dem Motto #BreakTheBias. Anlässlich dieses Feiertags beschäftige ich mich heute mit einem bekannten Bias, also einer kognitiven Verzerrung. Es geht um den sogenannten Confirmation Bias in der Forschung zu Risikotoleranz bzw. Abneigung gegen Risiko (Risikoaversion).

Überall liest man, dass Frauen risikoaverser sind als Männer. Es gibt unzählige volkswirtschaftliche Studien, die dieses Ergebnis mit Hilfe von standardisierten Laborexperimenten bestätigen. Welche Probleme diese Studien mit sich bringen, habe ich bereits letztes Jahr anlässlich des Weltfrauentags ausführlich beleuchtet.

Aufbauend auf diesen Betrachtungen möchte ich nun im Detail darauf eingehen, warum auch methodisch solide wissenschaftliche Ergebnisse, die Unterschiede bei der durchschnittlichen Risikoaversion zwischen den Geschlechtern finden, trotzdem oft einen falschen Eindruck der Realität vermitteln. Dabei geht es einerseits um methodisch korrekte statistische Analysen und andererseits um linguistische Präzision. Fangen wir mit letzterem an, denn dann ist die Mathematik auch einfacher zu verstehen.

Von der Natur der Dinge

Was hältst du von den folgenden zwei Aussagen?

• Vögel legen Eier
• Kanadier sind Rechtshänder

Während die erste Aussage uns korrekt vorkommt, ist die zweite Aussage offensichtlich Quatsch. Obwohl die Mehrheit der Kanadier rechtshändig ist, würden wir so einen starken Verkürzung einer statistischen Aussage intuitiv nicht zustimmen. Bei Vögeln ist es genau andersherum. Wenn man davon ausgeht, dass es ungefähr gleich viele männliche und weibliche Vögel gibt, einige davon aber unfruchtbar oder noch nicht geschlechtsreif sind, dann legt genaugenommen nur eine Minderheit aller Vögel tatsächlich Eier. Trotzdem haben wir intuitiv kein Problem mit der obigen Aussage. Es liegt für uns in der Natur des Dings „Vogel“, Eier zu legen.

Wenn wir ein Tier sehen, das Eier legt, dann ist dieses Verhalten ein Indiz dafür, dass es sich um einen Vogel handeln könnte. Da auch Amphibien wie manche Schlangen oder auch viele Fische Eier legen, reicht uns diese eine Tatsache natürlich noch nicht aus. Aber es wäre ein Start, der beim Eingrenzen der Art des Tieres hilft. Es würde hingegen niemand jemals versuchen, die Händigkeit einer Person als Startpunkt für die Bestimmung seiner Nationalität zu nutzen.

Herausragende Durchschnittlichkeit

Nimm als weiteres Beispiel folgende Aussage: „Frauen sind kleiner als Männer“. Was genau ist damit eigentlich gemeint? Vielleicht hat hier ein Journalist eine wissenschaftliche Studie aufgegriffen, in der die statistische Aussage getroffen wurde, dass „die durchschnittliche Körpergröße von Frauen statistisch signifikant geringer ist als die durchschnittliche Körpergröße von Männern“. Diese Aussage ist natürlich länger und klingt komplizierter. Daher wird oft vereinfacht, wenn über Wissenschaft geschrieben wird. Das ist bei Texten außerhalb der Forschung natürlich nachvollziehbar, aber je nach Kontext leider auch oft problematisch. Denn zu starke Verkürzungen können den Kern von wissenschaftlichen Aussagen sogar verfälschen oder Tatsachen in einem ganz anderen Licht erscheinen lassen.

Die Wissenschaftlerin Julie Nelson zeigt in einer Analyse, dass auch Wissenschaftler, die doch eigentlich gewohnt sein sollten, auf methodisch fundierte Weise zu arbeiten, ihre eigenen Ergebnisse selbst in ihren Arbeiten häufig unzulässig verkürzen. Die Diskussion der Forschungsergebnisse und entsprechende Empfehlungen der Forscher für die Praxis bauen somit teilweise auf vermeintlichen Erkenntnissen auf, die in den Daten gar nicht in der Form/Größenordnung zu finden waren. Sie vermutet dahinter Confirmation Bias bei den Wissenschaftlern, die einige Stereotype eben auch schon so oft gehört haben, dass sie diese von vorneherein als Wahrheit akzeptieren. Daher hinterfragen sie ihre eigenen Ergebnisse gar nicht mehr wirklich. Wer sich sicher ist, dass etwas wahr sein muss, findet durch entsprechende Analysen oft auch Daten, die genau diesen Glauben bestätigen. Schon der Volksmund warnt: Traue nie einer Statistik, die du nicht selbst gefälscht hat.

Wie sind statistische Unterschiede von Durchschnitten zu interpretieren?

Würdest du dir zutrauen, basierend auf der Körpergröße einer Person ihr Geschlecht zu raten?

Für eine Person, die 1,75m groß ist, ist die Chance, beim Raten des Geschlechts richtig zu liegen, ziemlich gering. Dann kannst du auch gleich eine Münze werfen und hast eine ähnliche Chance, richtig zu liegen. Wenn jedoch jemand so wie ich nur 1,60m groß ist, dann ist deine Chance mit der Antwort „Frau“ richtig zu liegen, relativ hoch. Das liegt daran, dass sich der Durchschnittswert von Frauen und der Durchschnittswert von Männern bei der Körpergröße statistisch signifikant voneinander unterscheiden. Das sieht man auch in der Grafik auf einen Blick:

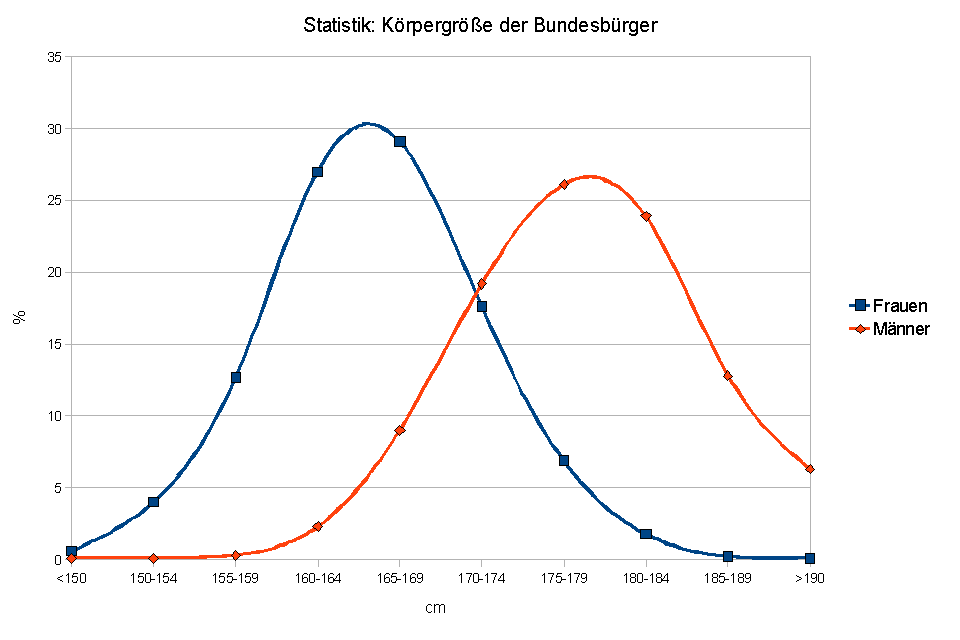
Was heißt statistisch signifikant?

Allerdings bedeutet das Wort „signifikant“ in diesem Kontext nur, dass der festgestellte Unterschied zwischen den Durchschnitten nicht auf reinen Zufall zurückzuführen sein kann. Es bedeutet aber nicht unbedingt, dass der Unterschied groß ist. Umgangssprachlich verstehen wir unter einem „signifikanten Unterschied“ meist, dass dieser nicht zufällig und groß ist. Letztere Aussage erforderte aber zusätzliche statistische Tests. So kann man die Größe des Unterschieds mit der Kennzahl Cohens d quantifizieren.

Cohens d misst die Größe des Unterschieds („Effektstärke“)

Cohens d für die Unterschiede in der durchschnittlichen Körpergröße liegt bei ungefähr 2,6. Alles über d>0,8 kann grob gesprochen als großer Unterschied interpretiert werden. Bei einem Wert von d=3 wäre die Chance, richtig zu raten bei 93% (bei einer angenommenen Normalverteilung). Wenn d=1 ist, liegt die Chance, richtig zu raten, noch bei 69% (verglichen mit 50% Chance, wenn man seine Vermutung einfach auf Basis eines Münzwurfs trifft).

Bei d=0,3 läge die Chance, durch die Zusatzinformation (z.B. Körpergröße) richtig zu raten, nur noch bei 56%. In diesem Fall bietet die Information, die du für das Ratespiel zur Verfügung hast, kaum einen Vorteil. Anders gesagt, überlappen sich die beiden Verteilungen stark. Und obwohl sich die Durchschnitt der beiden Gruppen statistisch signifikant, also nicht nur zufällig, voneinander unterscheiden, ist der Unterschied zwischen den Durchschnitten in diesem Fall ziemlich klein. Die Unterschied innerhalb der Gruppen (z.B. Männer / Frauen) sind hingegen vergleichsweise groß (d.h. grafisch, die Kurven sind eher breit).

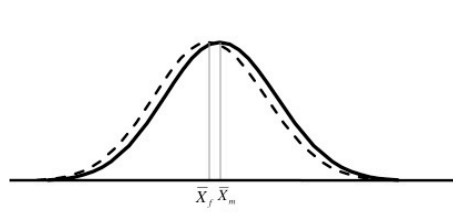
Wie können wir unser Chancen beim Geschlechter-Ratespiel erhöhen?

Wenn du zur Körpergröße vielleicht noch ein oder zwei weitere Datenpunkte (z.B. Bestzeit beim 100m Sprint, Hüftumfang) dazubekommen würdest, würdest du dich wahrscheinlich recht sicher fühlen beim Erraten des Geschlechts einer Person. Denn die Kombination von mehreren Informationen, die jeweils Verteilungen mit hohen Cohens d, also nur wenig überlappende Verteilungen, aufweisen, erhöhte die Wahrscheinlichkeit, richtig zu liegen.

Würde dir statt der 100m Zeit die Risikoaversion einer Person im Körpergrößen-Geschlecht-Ratespiel weiterhelfen? Intuitiv ist klar: Dieser Datenpunkt hilft eher nicht weiter. Das heißt grafisch ausgedrückt, dass die Verteilung der Risikoaversion von Frauen und von Männern sich stark überlappen. Die oben gezeigten Verteilungen der Körpergröße überlappen sich zwar auch, aber deutlich weniger stark als die Verteilungen der Risikoaversion.

Sind Frauen tatsächlich viel risikoaverser als Männer?

Sieht man von den methodischen Problemen volkswirtschaftlicher Studien zum Thema Risikoaversion ab, die ich letztes Jahr näher beleuchtet habe, lässt sich durchaus die Aussage treffen, dass die durchschnittliche Risikoaversion von Frauen (in Lotteriespielen im Labor) größer ist als die durchschnittliche Risikoaversion von Männern. Auch wenn man realitätsnähere Experimente anschaut oder tatsächliches Investmentverhalten (z.B. Assetallokation in Depots) betrachtet, zeigt sich, dass es nicht nur zufällige (=statistisch signifikante) Unterschiede zwischen der durchschnittlichen weiblichen und männlichen Risikoaversion gibt. Allerdings wird leider selten analysiert, wie groß der Unterschied zwischen den beiden Durchschnitten (oder dem Median der beiden Gruppen) tatsächlich ist und ob die Größe des Unterschieds statistisch signifikant ist.

In einer Re-Analyse bereits in wissenschaftlichen Magazinen veröffentlichter Artikel und Daten zum Thema „Geschlechterunterschiede bei der Risikoaversion“ zeigte Julie Nelson, dass sich meist nur ein kleiner Effekt (d<0,5) und maximal ein mittelgradiger Effekt (d bis 0,8) feststellen ließ. Richtig wäre also zu sagen: Frauen sind durchschnittlich ein wenig risikoaverser als Männer. Diese eingeschränkte Aussage eignet sich aber einfach nicht so gut als Schlagzeile.

Liegt es in der Natur von Frauen risikoaverser zu sein, genauso wie es in der Natur von Vögeln liegt, Eier zu legen?

Kritischer ist es, wenn nicht nur Journalisten, sondern Wissenschaftler selbst die eigenen Forschungsergebnisse (bewusst oder unbewusst) verkürzen, zuspitzen oder übertreiben. Dafür gibt es viele Gründe:

Zunächst ist es nicht nur in der Forschung zu Risikoaversion, sondern ganz allgemein in allen wissenschaftlichen Disziplinen, eindeutig nachweisbar, dass nicht signifikante Ergebnisse eine geringere Chance haben, veröffentlicht zu werden. Daher verstärken sich vorherrschende Meinungen tendenziell mit der Zeit. Wenn ich das Ergebnis erhalte, das ich erwartet habe, hinterfrage ich es meist nicht mehr ausreichend:

• Ist das durchgeführte (Labor-)Experiment überhaupt ein valider Test, um die Aussagen über die Natur der Dinge zu machen, die ich gerade treffe?
• Welche Größenordnung hat der gefundene Unterschied zwischen den Durchschnitten überhaupt? Wie stark überlappen sich die Verteilungen der beiden Gruppen?
• Ist meine Befragung / Experimentteilnehmer repräsentativ? Habe ich alle anderen relevanten Variablen berücksichtigt, die neben dem Geschlecht einen Unterschied zwischen den Gruppen erklären könnten (z.B. Alter, Einkommen, Bildungsstand, Familienstand)?

Wenn ein Forscher überzeugt ist, dass es in der Natur von Frauen liegt, risikoaverser zu sein, wird er seine Interpretation der Ergebnisse und Empfehlungen auf Basis dieser Überzeugung formulieren. Dieser Bias kann zu unbewussten Verkürzungen, ungenauen Formulierungen und unsinnigen Empfehlungen führen. Und in der Konsequenz leider auch dazu, dass sich eine selbsterfüllende Prophezeiung ergibt. Je häufiger man als Frau davon liest, dass Frauen risikoaverser sind, desto stärker ist die Gefahr der Stereotypisierung.

Stereotype Threat – und was du dagegen machen kannst

In der Psychologie bezeichnet man mit dem Begriff Stereotype Threat den Effekt, dass bestimmte soziale Gruppen durch die Angst, ein Vorurteil über ihre eigene Gruppe zu bestätigen, tatsächlich entsprechendes Verhalten zeigen. Zum Beispiel führt die Angst davor, das Vorurteil zu bestätigen, dass Frauen schlecht in Mathe sind, tatsächlich zu schlechteren Testleistungen. Das funktioniert allerdings auch andersherum: Erinnert man asiatische-amerikanische Frauen vor einem Mathetest nicht an ihr Geschlecht, sondern an ihre Abstammung, schneiden sie besser ab, da es das Vorteil gibt, dass Asiaten gut in Mathe sind.

Mein Wunsch: Let’s Break The Bias! Lasst uns weniger darüber sprechen, dass Frauen (ein bisschen) risikoaverser sind. Und ganz aufhören, zu spekulieren, warum das so sein könnte. Klare wissenschaftliche Erkenntnisse gibt es zu dieser Frage nach dem Warum? derzeit sowieso nicht.

Stattdessen lässt sich Stereotype Threat vielleicht sogar positiv nutzen. Denn immerhin gibt es inzwischen auch viele Artikel darüber, dass weibliche Investoren im Durchschnitt eine höhere Rendite erzielen. Vielleicht liegt das ja daran, dass sie ein wenig risikoaverser sind? 😉

Warst du selbst schon einmal in einer Situation, in der du Stereotype Threat gespürt hast? Hast du – rückblickend betrachtet – auch schon einmal Confirmation Bias unterlegen? Welche anderen Biases sind dir beim Thema Finanzen schon begegnet?